THE REASON BEHIND THE CATCHPHRASE

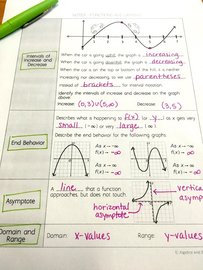
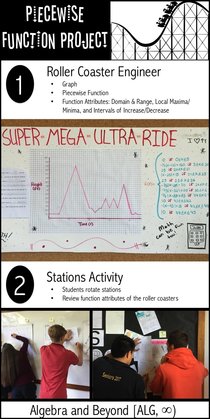
​Let’s start at the bottom, of Bloom’s Taxonomy that is. We all know that knowledge, aka recalling information, is the basic cognitive level of Bloom’s. Often my students want me to teach in a way so they can memorize the math steps. They think this means they understand what they are doing. Um, no, it definitely does not. Below is a video I show my students every year, so they can recognize that knowledge does not equal understanding. My students are pretty mind blown by the video, for many reasons, as you will see.
 

---

If this is the first time you have seen the backwards bicycle video, it's pretty neat, right?!

​I have discovered that if I can get my students to make the connection between knowledge and understanding, then they can jump to any other level of Bloom’s quite easily. I ask them to think of this connection like a hurdle or a hill; knowledge is on one side and understanding on the other. Once they get over that first obstacle, all of the other doors open to each higher level of cognitive thinking, and not necessarily in a particular order. I've seen students go directly from understanding to creating. It's really fascinating to watch students make these connections so quickly!
​
Bottom line, math cannot be just steps and numbers to students. Quite frankly, they enjoy it on the "understanding" side of the hill because that’s where they appreciate math and can make real world connections. But, getting them over that first hurdle is the first step and I’m glad I (and you) can help them connect knowledge with understanding – one lesson at a time.

​Examples of cognitive levels in terms of math:

• Knowledge – identifying the steps on how to solve, factor, evaluate, etc.
• Understanding – describe what we are looking for and why – zeros, vertex, intersection, etc.
• Apply – solve an equation or draw a graph
• Analyze – compare, contrast, and classify different functions
• Evaluate – explain and defend your solution
• Create – write your own problem

​For more teaching ideas and instant access to the Algebra and Beyond Resource Library, join the the mailing list!

Sign me up!